| 论文英文名字 | BatFL: Backdoor Detection on Federated Learning in e-Health |
|---|---|
| 论文中文名字 | BatFL:电子健康中联邦学习的后门检测 |
| 作者 | Binhan Xi, Shaofeng Li, Jiachun Li, Hui Liu, Hong Liu, Haojin Zhu |
| 来源 | 29th IWQoS 2021: Tokyo, Japan [CCF 计算机网络 B 类会议] |
| 年份 | 2021 年 6 月 |
| 作者动机 | |
| 阅读动机 | |
| 创新点 | 基于联盟博弈和 Shapley 值的思想,提出了一种有效的、实时的 FL 后门检测系统。 |
内容总结
主要贡献
- 在电子医疗场景中提出了对联邦学习的广泛后门攻击。该攻击是对具有敏感和私人患者数据的电子医疗 FL 的第一次攻击。它显示出很高的成功率,并且很难检测到。
- 通过将 FL 建模为联盟博弈,通过 Shapley 值提出了一种新颖的后门容忍 FL 框架 BatFL。与其他最先进的文献相比,BatFL 的表现更好。此外,BatFL 在单个和多个恶意客户端设置中都有效。
- 在文本和图像领域的各种机器学习任务上实现了 BatFL。实验结果表明,该算法能够成功阻止电子健康应用中对 FL 的后门攻击。
威胁模型
- 攻击者完全访问某些医院的本地患者数据集;
- 攻击者完全访问局部模型体系结构和训练过程。
挑战
- 训练过程中实时检测困难。
- 攻击的多样性。
- 检测效率。
BatFL 设计
动机:训练机制表现出多个客户端合作完成特定任务的特征。
联盟博弈
在博弈论中,联盟博弈是由整个参与者联盟中的每个小群体被分配一定的效用值的行为给出的。
形式上,联盟博弈由局中人组成的有限集合 N(称为大联盟)和一个特征函数或效用函数 $v:2^N\rightarrow\mathbb{R}$ 组成,该特征函数或效用函数将所有可能的由玩家分组的小联盟映射到一个“奖励”集,并且满足性质 $v(\emptyset)=0$。该函数描述了大联盟中的玩家通过组建小联盟可以获得的“奖励”。
Shapley 值
给定一个联盟博弈 (N, v),其中 N 是系统中的代理数量,v 是效用函数,衡量如果一组代理 S 在联盟博弈中合作,将产生多少收益。在联邦学习中,一个参与节点的 Shapley 值能够评估该节点对聚合的最终模型的边际贡献量。
每个玩家 i 的 Shapley 值:
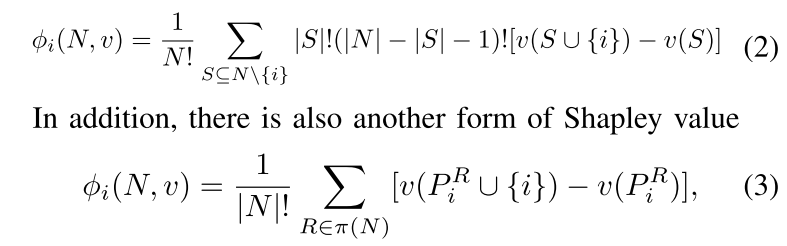
BatFL 机制设计
首先,我们将整个联邦学习框架建模为联盟博弈(N,v),其中 N 是联邦学习的每个参与者,包括良性客户端和潜在攻击者,v 定义为如果一组客户端 S 形成联盟,然后将上传的参数进行聚合,其在中央服务器上的测试集准确率。
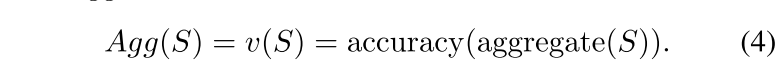
然后计算每个客户端的 Shapley 值。在第 t 轮的训练中,基于公式 3,客户端 i 的 Shapley 值可以计算为:
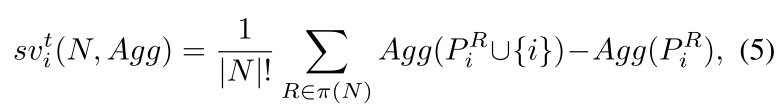
问题 1:因为随着全局模型的收敛,攻击者和良性客户端之间的差异往往会变得微妙。
解决办法:计算了从开始到本轮累计的 Shapley 值,作为衡量贡献度的标准。
第 t 轮客户端 i 的累积 Shapley 值可以计算为:
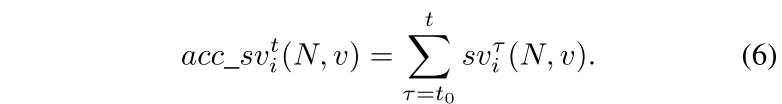
问题 2:当联邦学习第一次开始时,上传的参数受到本地初始化随机化的影响,因此前几个参数不是很有代表性。
解决办法:选择某个轮次 $t_0$,比如 5 到 10 个轮次,然后开始累积操作。
实现

- 计算一轮的 Shapley 值
- 计算长期的 Shapley 值
- 通过 MAD 计算异常指数并检测攻击者
中位数绝对偏差和异常指数
在统计学中,中位数绝对偏差是对单变量数值型数据的样本偏差的一种鲁棒性测量。其定义为

因此,MAD 衡量了整个数据相对于中位数的差异性,我们可以利用 MAD 得到的异常指数衡量每个数据点相对于系统“中心”的偏差,从而找出异常值来消除。 具体步骤如下:
- 假设样本
$X={X_1,X_2,...,X_n}$,计算每个输入样本的中值$\tilde{X}=median(X)$; - 计算单个数据点
$X_i$与整个中位数之间的绝对偏差$|X_i−\tilde{X}|$; - 计算绝对偏差的中值
$MAD=median(|X_i−\tilde{X}|)$; - 将数据点和中位数之间的每个偏差除以 MAD,我们可以根据 MAD 得到所有数据点和数据中心之间的距离
$m_i$,也称为异常指数; - 基于
$m_i$,我们去除距离数据中心的距离大于阈值的异常值来实现检测。
如果一个数据点的异常指数大于 2,则它有超过 95% 的置信度是异常值。
开销优化
问题:在公式 3 中存在阶乘运算和全排列运算,当用户数 n 较大时,这些运算可能带来不可接受的 $O(n!)$ 时间复杂度。
解决办法:取样。
具体过程:
- 准备采样源
$P$,它是 N 个玩家的全排列集合$P=\pi(N)$; - 从
$P$中取出 m 个样本,概率为$\frac{1}{|N|!}$形成一个集合$M$; - 对于每个样本 x,计算 i 的边际贡献
$C_i(x)=v(P_i^x\cup{i})−v(P_i^x)$,其中$P_i^x$是以 i 结束并排列为 x 的玩家集合; - 对于所有样本,平均每个玩家的边际贡献,得到它们的近似 Shapley 值:
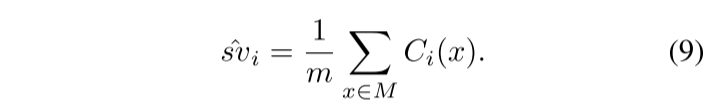
实验
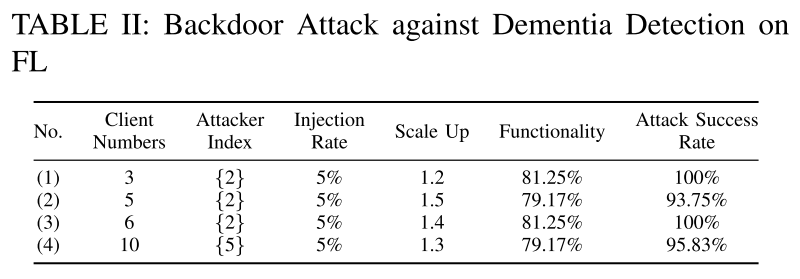
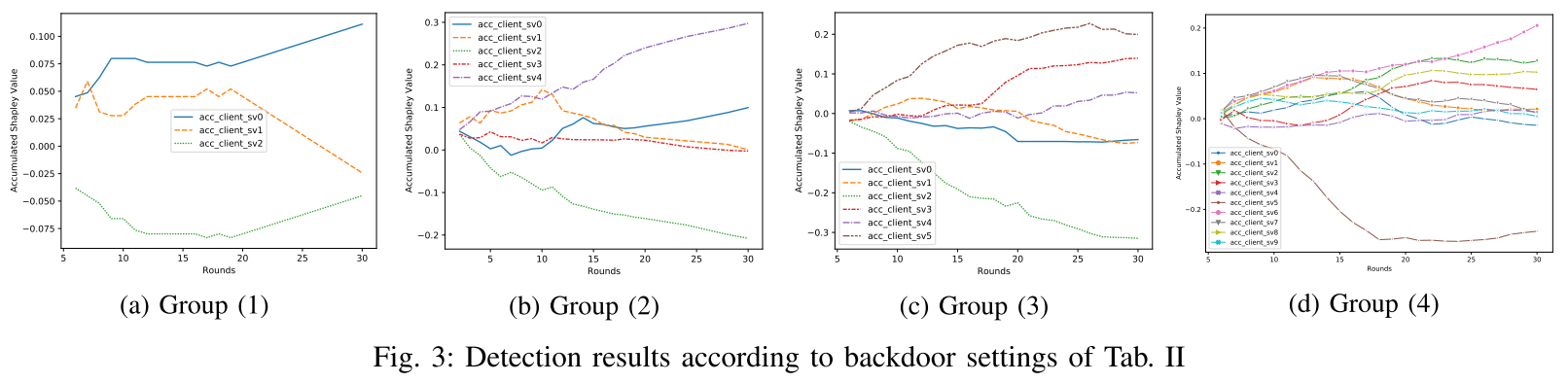
- 组 (1)∼(3) 的客户端 2 和组 (4) 的客户端 5 是后门攻击者
- 后门攻击者的累积 Shapley 值不同于同一组中的其他良性客户端
和 (5) 中带-不带累积机制的Shapley值.png)
- 在没有累加操作的情况下,攻击者的 Shapley 值与良性攻击者没有很大的区别。
- 攻击者和良性客户端之间的累积 Shapley 值的差异很大
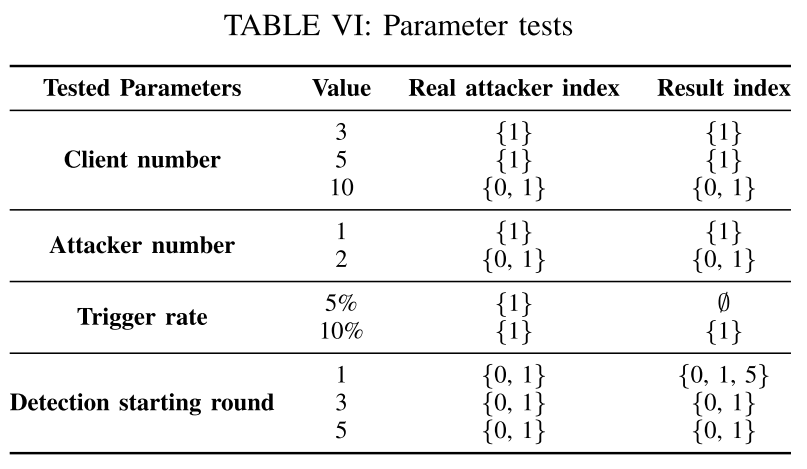
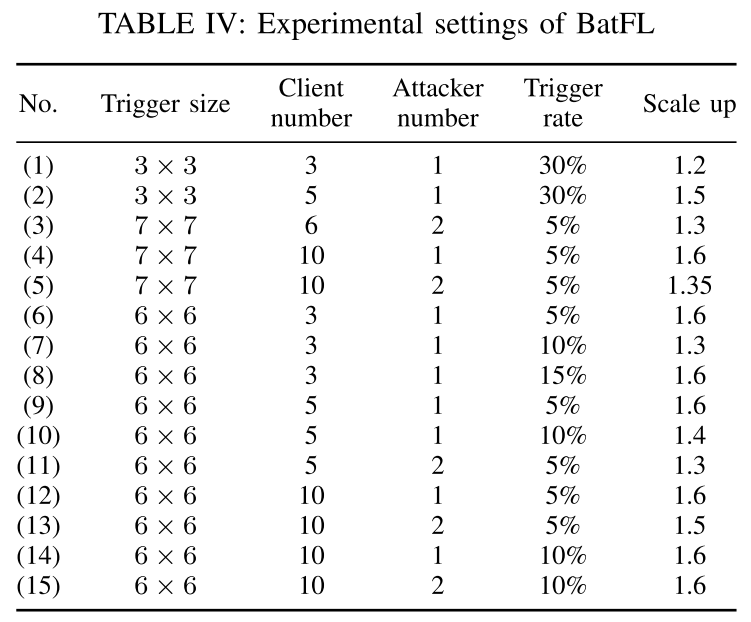
- 客户端数量、攻击者数量、触发器率和检测开始轮次
- 该算法能够成功检测出大部分攻击
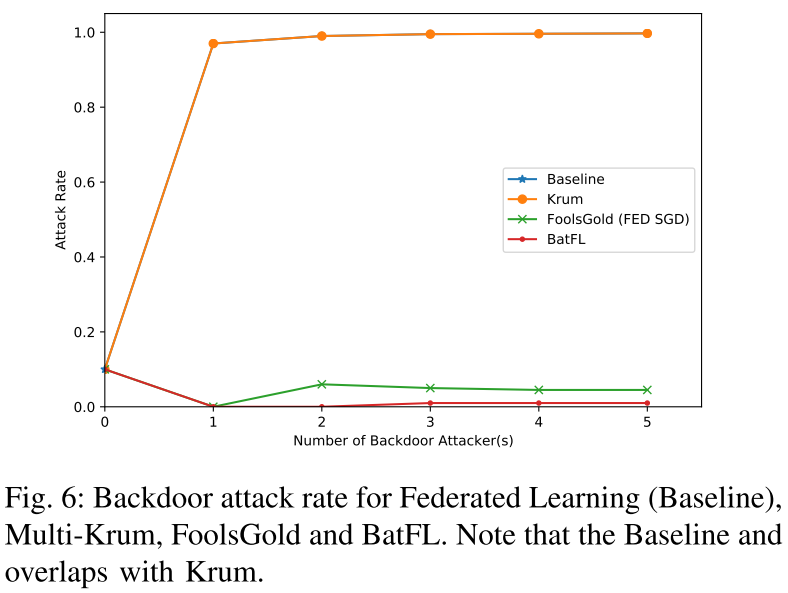
- 只要攻击者的数量增加,BatFL 和 FoolsGold 的表现都比 Krum 好得多。
总结
在本文中,我们对基于 FL 的 e-Health 系统进行了第一次有效的后门攻击,并提出了一种新的后门容忍的联邦学习框架 BatFL。为了检测来自良性客户端的后门攻击者,BatFL 利用 Shapley 值,使其在 FL 框架上更加有效。在 FL 上的文档和图像分类任务都证明了我们的 BatFL 能够以可接受的性能开销有效地消除对 FL 系统的后门攻击。
