Local Model Poisoning Attacks to Byzantine-Robust Federated Learning

bid000 于 2022-06-14 发布
论文英文名字 Local Model Poisoning Attacks to Byzantine-Robust Federated Learning
论文中文名字 拜占庭鲁棒联邦学习的局部模型中毒攻击
作者 Minghong Fang, Xiaoyu Cao, Jinyuan Jia, Neil Zhenqiang Gong
来源 29th USENIX Security Symposium 2020
年份 2020 年 8 月
作者动机 目前的主要攻击集中在对数据中毒攻击，但缺少对本地训练过程中的模型中毒攻击的研究，尽管有，也是不抗拜占庭攻击联邦学习的场景下，本文是第一次研究在抗拜占庭攻击的联邦学习场景下的局部模型中毒攻击
阅读动机
创新点 将寻找精心设计的局部模型表述为优化问题

内容总结

主要贡献

  1. 首次对攻击拜占庭鲁棒联邦学习进行了系统研究。
  2. 提出了针对拜占庭鲁棒联邦学习的局部模型中毒攻击。我们的攻击是在学习过程中操纵受损工作设备上的本地模型参数。
  3. 推广了两种针对数据中毒攻击的防御方法，以抵御局部模型中毒攻击。我们的结果表明，尽管其中一种方法在某些情况下有效，但在其他情况下成功率有限。

拜占庭鲁棒联邦学习

拜占庭鲁棒的联邦学习是指的在联邦学习参与者存在不可信的情况下，如何保障联邦学习的安全运行。这里要提到拜占庭将军问题，就是非常经典的分布式情况下如何保证通信有效性。因此拜占庭鲁棒的联邦学习实际上就是那些采用了拜占庭鲁棒聚合规则的联邦学习，而采用了最简单的求均值的聚合规则就是不抗拜占庭攻击的联邦学习。

拜占庭鲁棒的聚合规则

Krum 在 m 个局部模型中选择一个与其他模型相似的模型作为全局模型。

Krum 的想法是即使所选择的局部模型来自受破坏的工作节点设备，其能够产生的影响也会受到限制，因为它与其他可能的正常工作节点设备的局部模型相似。

Bulyan 本质上是 Krum 和修整均值的变体结合。

Bulyan 首先迭代应用 Krum 来选择 θ（θ ≤ m-2c）局部模型。然后，Bulyan 使用修整均值的变体汇总 θ 个局部模型。

该聚集规则独立地聚集每个模型参数。具体地，对于每个第 j 个模型参数，主设备对 m 个局部模型的第 j 个参数进行排序。删除其中最大和最小的 β 参数，计算其余 m-2β 的平均值作为全局模型的第 j 个参数。

在中位数聚合规则中，对于第 j 个模型参数，主设备都会对 m 个局部模型的第 j 个参数进行排序，并将中位数作为全局模型的第 j 个参数。当 m 为偶数时，中位数是中间两个参数的均值。与修整均值聚集规则一样，当目标函数为强凸时，中位数聚集规则也能达到阶优误差率。

威胁模型

局部模型中毒攻击

想法：通过在联邦学习的每次迭代中精心制作从受感染的工作设备发送到主设备的本地模型来操纵全局模型。

优化问题

优化问题：攻击者的目标（本文称其为有向偏离目标）是使全局模型参数最大程度地偏离全局模型参数在没有攻击的情况下沿其变化的方向的反方向。假设在迭代中，$w_i$ 是使用第 i 个工作节点设备计划在没有攻击时发送给主设备的局部模型。假定前 c 个工作节点设备受到了破坏。有向偏差目标是通过在每次迭代中解决以下优化问题，为受损的工作节点设备制作局部模型：

优化问题

全知识：$w_1,...,w_c,w_{c+1},...,w_m$ 已知，直接求解优化问题

部分知识：$w_1,...,w_c$ 已知，用 $w_1,...,w_c$ 估计 $w$

聚合规则未知：猜测聚合函数

攻击 Krum

由于 Krum 是选择一个最接近的本地模型作为返回结果，那么就尽量在攻击时让联邦学习选择被感染的设备的本地模型。这种情况下一共分为两步。 首先，要让感染设备的本地模型偏差尽量大，其次，要让其他感染设备的本地模型都接近这个偏差值，这样方便联邦学习依照 Krum 原则对他进行选择，从而达到攻击目的。

挑战：优化问题的约束是高度非线性的，并且局部模型的搜索空间非常大。

解决办法：(1) $w_1^{'} = w_{Re}-\lambda s$ (2) 首先假设其他 c−1 个受感染的局部模型与 $w_1^{'}$ 相同，然后我们解 $w_1^{'}$ ，最后我们随机抽样 c−1 个向量，其到 $w_1^{'}$ 的距离最大为 $\epsilon$.

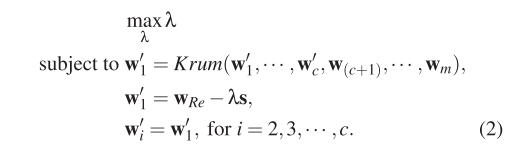
Krum全知识优化问题

  1. 计算 c 个攻击前局部模型的平均值
  2. 使用平均局部模型估计变化的方向
  3. 将受损工作设备上的攻击前本地模型视为良性工作设备上的本地模型

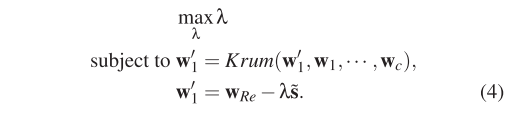
Krum部分知识优化问题

攻击 Trimmed Mean

如果 $s_j = -1$ ，在区间 [ $w_{max,j}$，$b\cdot w_{max,j}$ ]（$w_{max,j} > 0$）或 [ $w_{max,j}$，$w_{max,j} /b$ ]（$w_{max,j} <= 0$） 否则，我们在区间[ $w_{min,j} / b$，$w_{min,j}$ ]（$w_{min,j} > 0$）或[ $b\cdot w_{min,j}$，$w_{min,j}$ ]（$w_{min,j} <= 0$) 随机采样 c 个数。

挑战：（1）攻击者不知道变化的方向变量 $s_j$ ，因为攻击者不知道良性工作设备上的局部模型。（2）攻击者不知道良性局部模型参数的最大 $w_{max,j}$ 和最小 $w_{min,j}$。

解决办法：（1）使用受感染工作设备上的本地模型来估计变化的方向变量。（2）在受感染的工作设备上使用攻击前局部模型参数来估计 wmax、j 和 wmin、j。

攻击 Median

使用与 Trimmed Mean 相同的攻击方法来攻击 Median 聚合规则

实验

实验结果

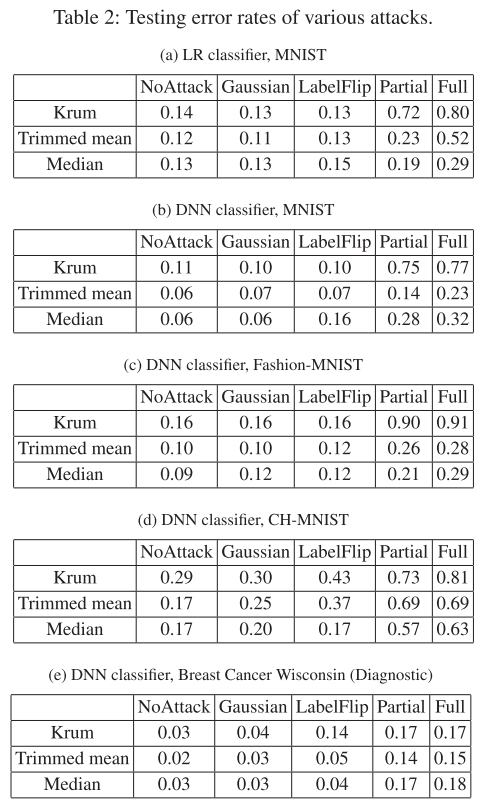
已知聚合规则

表 1 显示了在四个数据库上进行比较的攻击的测试错误率。
(1) 表明我们的攻击是有效的，并且大大优于现有的攻击。
(2) 除了在 Breast Cancer Wisconsin（Diagnostic）数据库上，Krum 与 Median 攻击的效果相当之外，Krum 对本文的攻击的鲁棒性不如均值和中位数高。

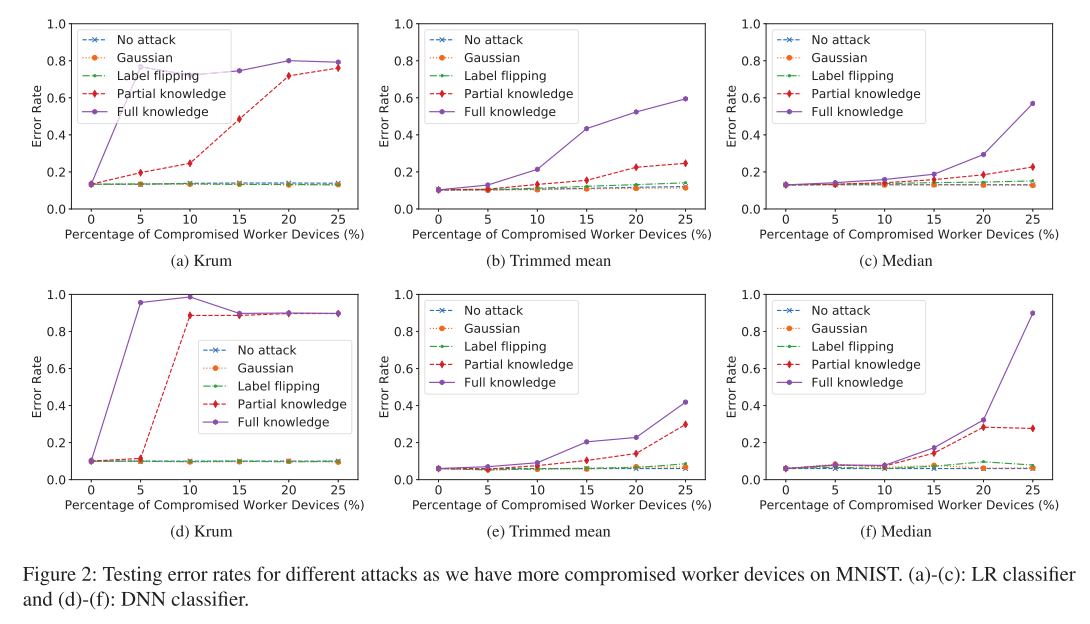
攻击者数量对错误率的影响

图 2 给出了随着 MNIST 上受到破坏的工作节点设备的百分比增加，不同攻击的错误率。 随着受到破坏的工作节点设备数量的增加，本文的攻击会大大提高错误率。作为基线对比的标签翻转攻击只会稍微增加错误率，而高斯攻击则对错误率没有产生明显的影响。 图 2 的实验中有两个例外是，当被破坏的工作人员设备的百分比从图 2a 中的 5％增加到 10％，以及，从图 2d 中的 10％增加到 15％时，Krum 的错误率降低。作者分析，这可能是因为 Krum 每次迭代都会选择一个局部模型作为全局模型。

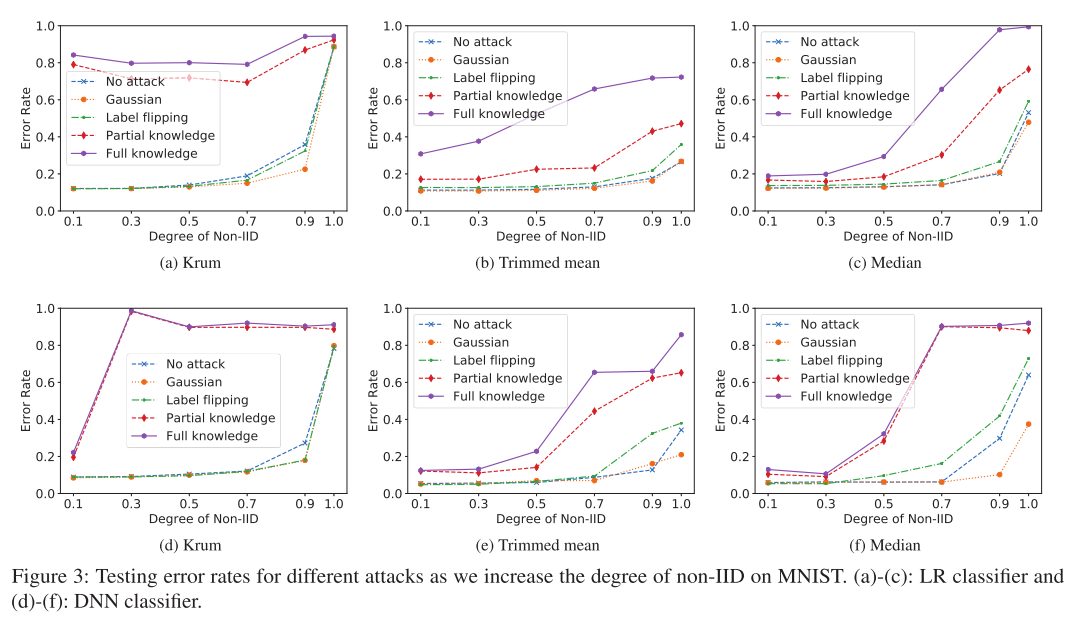
no-iid维度对错误率的影响

图 3 给出了针对 MNIST 上不同程度的非 IID 数据进行的攻击的错误率变化情况。包括无攻击在内的所有攻击的错误率都随着非 IID 程度的提升而增加，只有针对 Krum 的攻击的错误率会随着非 IID 的程度而波动。可能的原因是，由于不同工作节点设备上的局部训练数据集的非 IID 情况越来越严重，局部模型呈现更加多样化的分布状态，从而为攻击留下了更多空间。

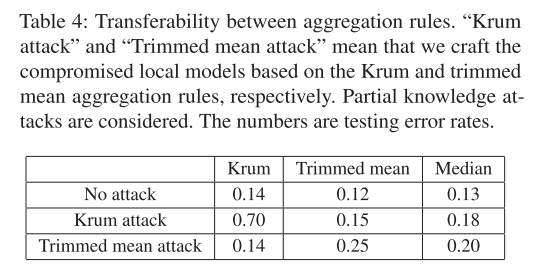
未知聚合规则

针对未知聚合规则，作者基于某一个聚合规则构建局部模型，之后通过实验验证分析其对其他聚合规则的攻击效果。表 2 显示了聚合规则之间的可转移性，其中也分别考虑了 MNIST 和 LR 分类器。「 Krum 攻击」和 「修整均值攻击」 表示分别基于 Krum 和修整平均聚合规则来构建受损的局部模型。本实验中考虑部分知识攻击。表中给出的数字结果是测试错误率。

防御

本文将用于防御数据中毒攻击的 RONI 和 TRIM 概括用于防御本文提出的的局部模型中毒攻击。

（1）基于错误率的拒绝（ERR）：删除了对全局模型的错误率具有较大负面影响的局部模型（受 RONI 的启发，后者删除了对模型的错误率具有较大负面影响的训练示例）
（2）基于损失函数的拒绝（LFR）：删除了对损失影响大的局部模型（受 TRIM 的启发，删除了对损失有较大负面影响的训练示例）。
（3）ERR 和 LFR 结合

防御结果

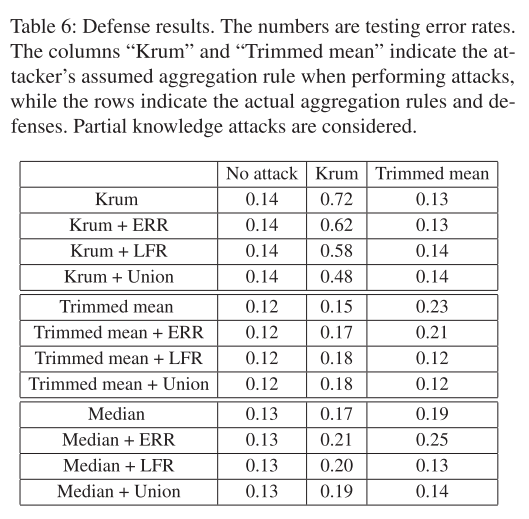
本实验中考虑部分知识攻击。表 3 的结果说明三方面问题：

  1. LFR 与 ERR 相当或比 ERR 更有效，即 LFR 的测试错误率与 ERR 相似或小得多。
  2. 在大多数情况下，Union 与 LFR 相当，但在一种情况下（Krum + LFR 对 Krum 和 Krum + Union 对 Krum），Union 更有效。
  3. LFR 和 Union 可以在某些情况下有效防御本文提出的攻击方法。

结论

  1. 寻找这种精心设计的局部模型可以表述为优化问题
  2. 我们需要新的防御措施来防御我们的本地模型中毒攻击