| 论文英文名字 | Can You Really Backdoor Federated Learning? |
|---|---|
| 论文中文名字 | 你真的可以后门联邦学习吗? |
| 作者 | Ziteng Sun, Peter Kairouz, Ananda Theertha Suresh, H. Brendan McMahan |
| 来源 | CoRR, November 2019 |
| 年份 | 2019 年 11 月 |
| 作者动机 | 对后门攻击和防御进行研究,选择(真实的,用户分区的和 no-iid 的)EMNIST 数据集 |
| 阅读动机 | |
| 创新点 | 允许非恶意客户机正确标记来自目标任务的样本 |
内容总结
后门攻击场景
- 对手的抽样
- 随机采样攻击:在客户端的随机抽样下,每轮中的对手数量遵循超几何分布。
$(0, min(\epsilon \cdot K, C \cdot K))$ - 固定频率攻击:每 f 轮出现一个对手。
$f = 1/(\epsilon \cdot C \cdot K$)
- 随机采样攻击:在客户端的随机抽样下,每轮中的对手数量遵循超几何分布。
- 后门任务
- 在后门攻击中,攻击者的目的是让模型在某些子任务上失败。本文允许非恶意客户端在目标任务中正确标注样本。
- 本文通过将多个选定的“目标客户机”的示例分组来形成后门任务。将目标客户端的数量称为“后门任务数量”,并探讨其对攻击成功率的影响。
模型更新中毒攻击
我们基于 (3; 4) 提出的模型替换范式,重点研究模型更新中毒攻击。当在第 t 轮中仅选择一个攻击者(WLOG假设它是客户端 1)时,攻击者试图通过发送后门模型 $\omega^*$ 来替换整个模型
$$\Delta \omega_t^1 = \beta(\omega^*-\omega_t)$$
其中 $\beta$ 是提升系数。
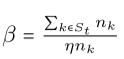
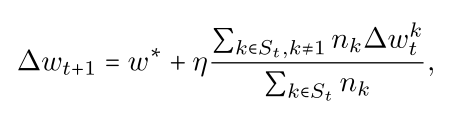
如果我们假设模型已经足够收敛,那么它将在 $\omega^*$ 的一个小邻域内,因此 k > 1 的其他更新 $\Delta \omega_t^k$ 很小。如果多个攻击者出现在同一回合中,则假定他们可以相互协调并平均划分此更新。
- 获取后门模型
- 一个描述后门任务的集合
$D_{mal}$ - 一个从真实分布生成的训练样本集合
$D_{trn}$
- 一个描述后门任务的集合
- 后门攻击
- 不受限制的增强后门攻击:用
$\omega^t$初始化,用$D_{mal} \cup D_{trn}$训练模型。(更新范数大,作为基线) - 范数限制后门攻击:通过使用多轮投影梯度下降训练模型,在每一轮中,我们使用无约束训练策略训练模型,并将其投影回
$\omega^t$周围大小为$M/\beta$的$\ell_2$球。
- 不受限制的增强后门攻击:用
防御
- 更新的规范阈值
假设对手知道阈值 M,因此总是可以返回这个量级的恶意更新。将这种强大优势赋予对手,使得范数边界防御等同于以下范数裁剪方法:
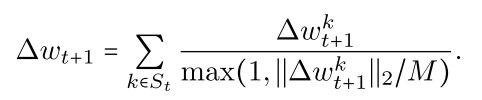
- (弱)差分隐私
首先裁剪更新(如上所述),然后添加高斯噪声。
实验
- 数据集:EMNIST 数据集(FEMNIST)
- 模型:具有两层卷积层,一层最大池层和两层稠密层(全连接层)的五层卷积神经网络
- 评估指标:主要任务准确率和后门任务准确率
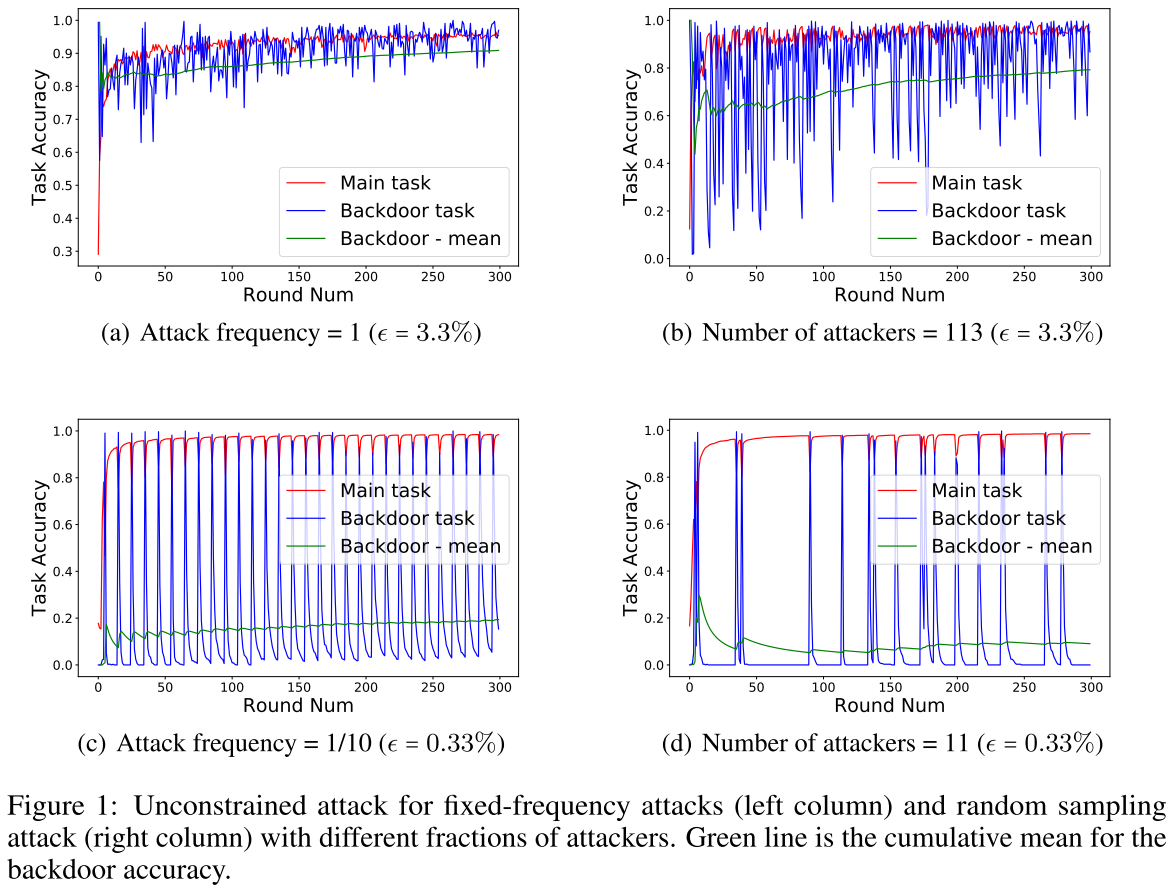
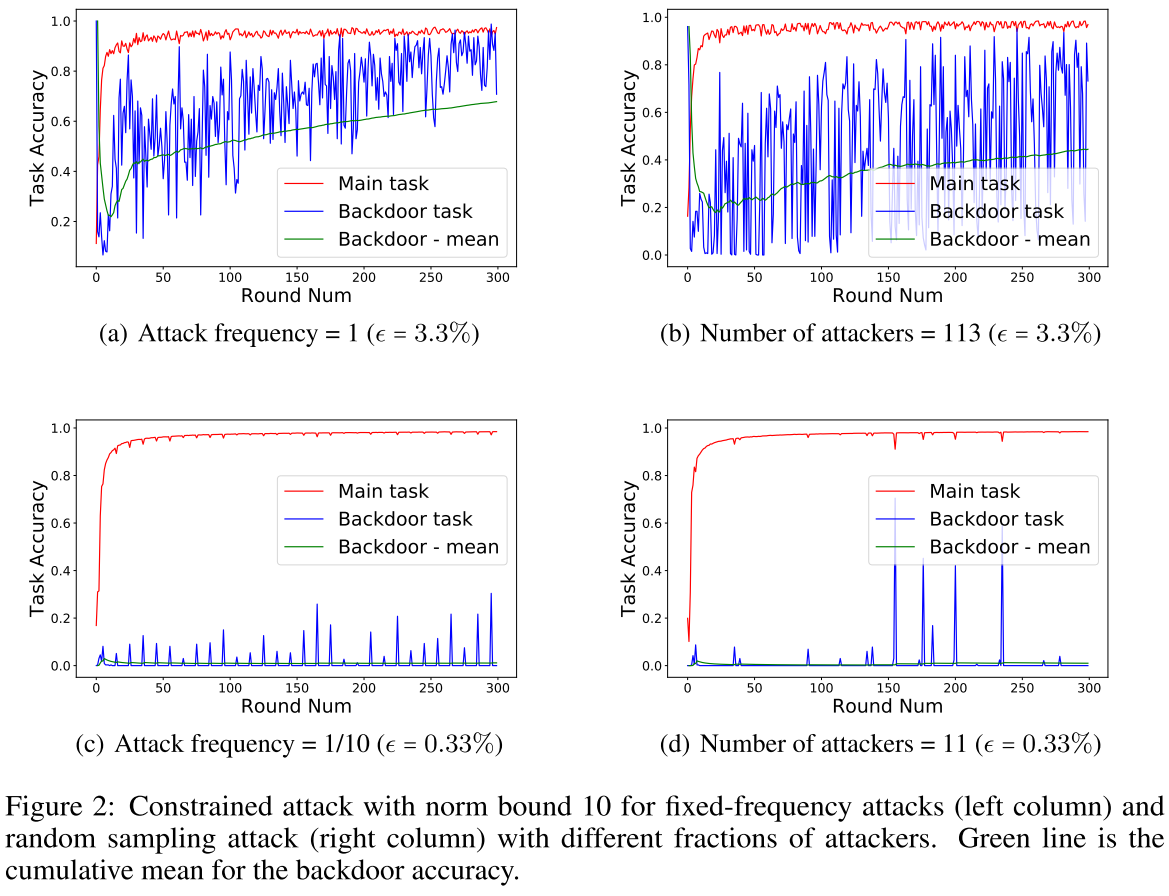
注:(1)图中绿色的线代表后门任务的平均准确率,准确率越高代表后门攻击越有效。 (2)左边一列为固定频率攻击,右边一列为随机采样攻击
- 固定频率攻击比随机采样攻击更有效
- 攻击频率越高,攻击越有效
- 攻击者数目越多,攻击越有效
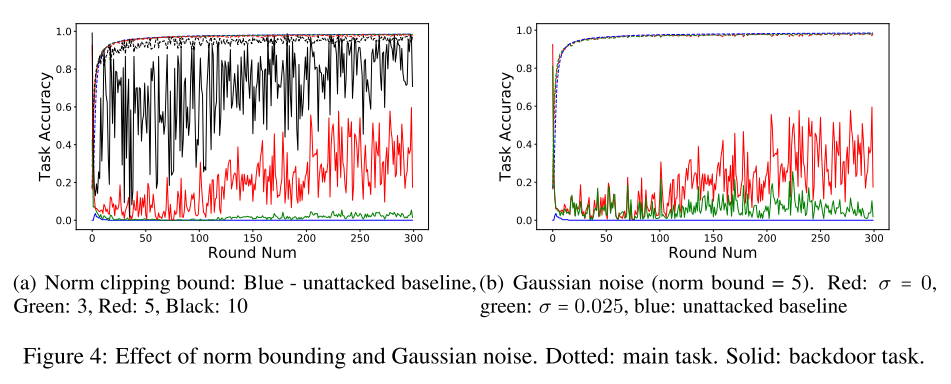
- 范数约束攻击对攻击起到一定的防御作用
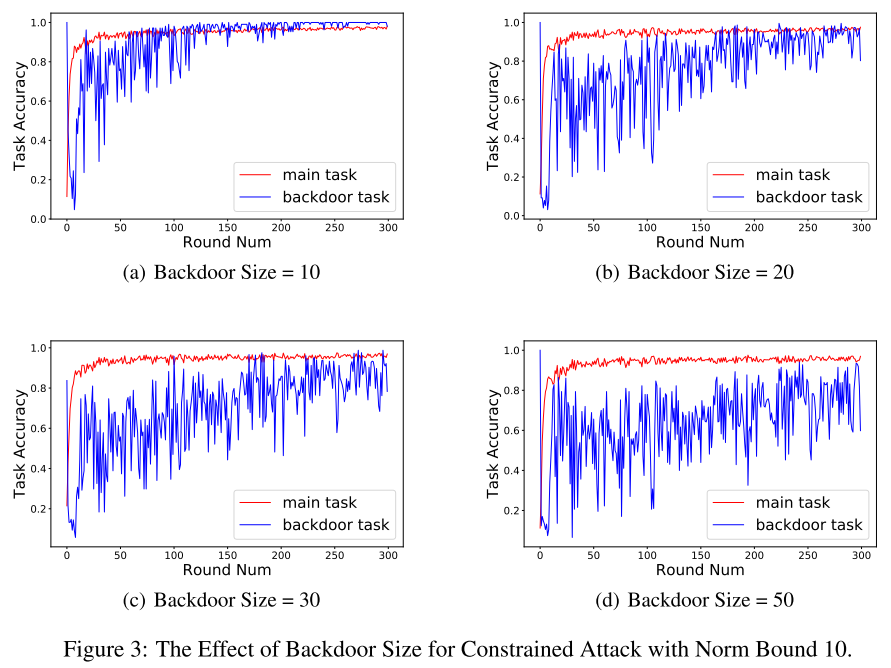
- 后门任务越多,适应恶意模型的难度就越大。
总结
- 本文在更现实的 EMNIST 数据集下研究了针对联邦学习的后门攻击和防御。
- 对手的数量和模型容量会影响后门攻击
