论文英文名字	NIKE-based Fast Privacy-preserving High-dimensional Data Aggregation for Mobile Devices
论文中文名字	基于 NIKE 的移动设备快速隐私保护高维数据聚合
作者	Kalikinkar Mandal, Guang Gong, Chuyi Liu
来源	CACR Technical Report, CACR 2018-10
年份	2018 年 10 月
作者动机	提高聚合方案的通信和计算效率，（1）密钥协商阶段的开销巨大，（2）秘密分享和恢复也很消耗时间。
阅读动机
创新点	（1）引入了 NIKE，在离线阶段计算 master key。这种方法比 D-H 协议更加高效； （2）对于 one-time pairwise key 的秘密分享采用 2-3 来取代 t-m。（正则图）

内容总结

主要贡献

1. 非交互式密钥建立协议
2. 基于 NIKE 的安全聚合协议
3. 实验评估和比较

预备知识

1. KDF
   （1）在密码学中，密钥派生函数 (KDF) 是一种加密散列函数，它使用伪随机函数从一个秘密值（如主密钥、密码或密码短语）中派生出一个或多个秘密密钥。
   （2）KDF 可用于将密钥扩展为更长的密钥或获取所需格式的密钥，例如将作为 Diffie-Hellman 秘钥交换结果的组元素转换为用于 AES 的对称密钥。
2. 单向函数
   单向函数 $F:{\{0, 1\}}^k \rightarrow {\{0, 1\}}^n$ 是一个易于计算且难以求逆的函数。

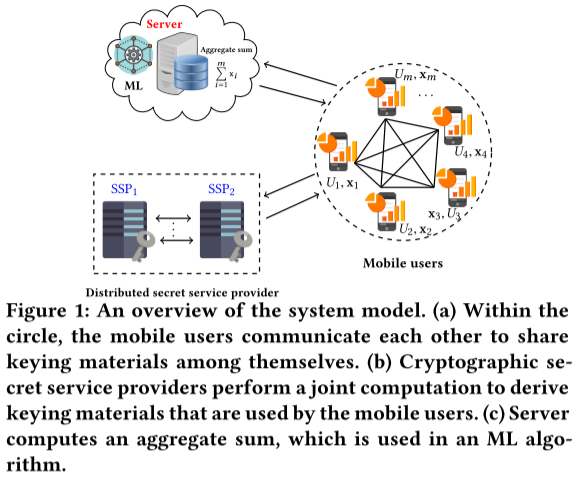
系统模型概述

• 系统中有 1 个服务器，用于聚合结果。
• 系统中有 m 个用户，每个用户有一个 r 维的数据 $x_i$。该系统的目标是让服务器只学习当前用户输入的总和 $\sum_ix_i$，而不是其他任何东西。
• 系统中有 2 个秘密服务提供商（SSP），组成分布式 SSP。

非交互式成对密钥建立方案

基本想法：使用双变量多项式以非交互方式在用户之间导出成对密钥，其中单变量多项式在两个SSP（即 SSP1 和 SSP2）之间秘密共享。我们使用一个特殊的二元多项式，它是一个单变量多项式与两个自变量的乘积。

• 非交互式成对密钥计算 (NPKC) 方案由三个算法的元组组成：
  
• 具体实现
  
• 用于生成 m 对秘密共享多项式的两方协议:
  其中，子协议 $\pi_{EXP}$ 的细节如下所示：
  

安全聚合方案

基本思路：在我们的设置中，聚合协议由两个阶段组成。在离线阶段，每个用户从两个 SSP 接收两对秘密共享多项式，用于导出将在聚合和协议中使用的密钥材料。每个用户还从服务器接收有关其 $l$ 正则通信网络邻居的信息。在在线阶段，服务器 S 与所有用户 U 运行聚合和协议，其中唯一的服务器接收聚合和作为输出。

• 单向密钥链

• 安全聚合协议

• Round 0：非交互式成对密钥计算（NIKE）
  • 每个用户从 SSPs 接收两对秘密共享多项式
  • 每个用户计算 $g_i(x)$ 和 $h_i(x)$
  • 每个用户计算自己和邻居节点的成对密钥 $MK_{i,j}$ 和 $EK_{i,j}$
• Round 1：由服务器发起聚合和计算
  • 服务器在 $[T_l,T_{l+1}]$ 发起聚合，并通知用户，活跃的用户 $U_0$ 响应服务器并参与聚合
  • 服务器广播 $(\mathcal{U}_0, \tau, T_l, TS_l)$ 和签名 ${\sigma}_s$
• Round 2：基于单向密钥链的成对密钥掩码然后加密输入
  • 验证签名和邻居节点数量
  • 计算自掩码的密钥
  • 计算其与邻居节点的成对密钥
  • 秘密分享 $MK$
  • 计算并秘密分享 ${\kappa}_i$
  • 计算成对掩码 $q_{i,j}$
  • 计算加双掩码后的输入 ${\alpha}_i$ 并发送给服务器
• Round 3：故障恢复信息交换
  • 用户收到加密的 shares 后解密并保存，一旦任何解密过程失败就中止
  • 服务器收到用户发送的 ${\alpha}_i$，用户记为 $\mathcal{U}_1$ 判断 $\mathcal{U}_1$ 中用户的数量是否大于 t，并发送给所有用户
  • 每个用户检查 $U_i\in\mathcal{U}_1$, $|\mathcal{U}_1| \geq t$, $\mathcal{U}_1 \subseteq \mathcal{U}_0$
  • 用户对 $\mathcal{U}_1$ 签名发给服务器
  • 服务器将收到签名的用户记为 $\mathcal{U}_2$ 并将签名发给 $\mathcal{U}_2$ 中的用户
  • 用户检查用户数量和邻居数量
  • 用户验证 $\mathcal{U}_2$ 中的所有用户的签名
  • 对于所有掉线的邻居用户，上传对应的 one-time pairwise key 的 shares；对于非邻居的掉线用户，上传 $\perp$；对于所有的在线用户，包括自己，上传关于 ${\kappa}_i$ 的 shares；
• Round 4：通过服务器计算聚合和（解密然后取消掩码）
  • 将收到消息的客户端记为 $\mathcal{U}_3$
  • $\mathcal{U}_0 = \mathcal{U}_3$ 没有用户掉线
    （1）验证 shares
    （2）重构 ${\kappa}_i$
    （3）计算聚合结果
  • $\mathcal{U}_3 < \mathcal{U}_3$ 有用户掉线 （1）验证 shares
    （2）重构 ${\kappa}_i$
    （3）重构 one-time pairwise key
    （4）计算聚合结果

性能分析

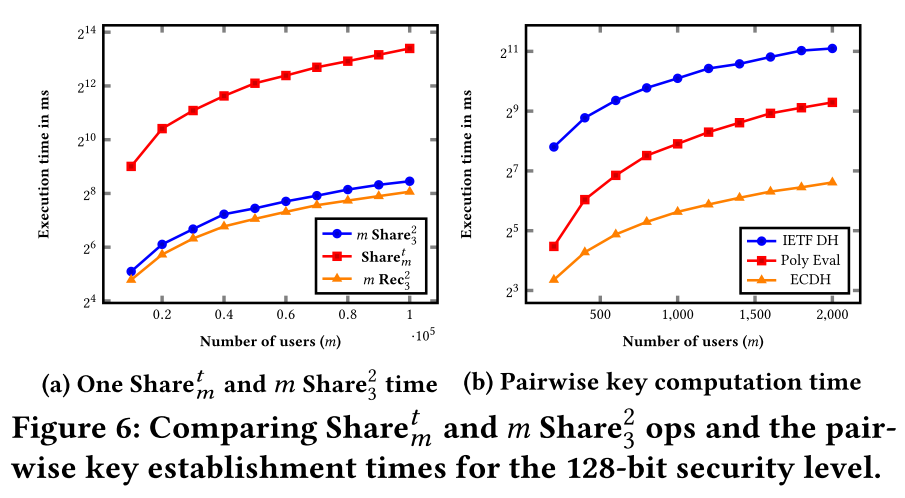
• 秘密分享和密钥协商性能

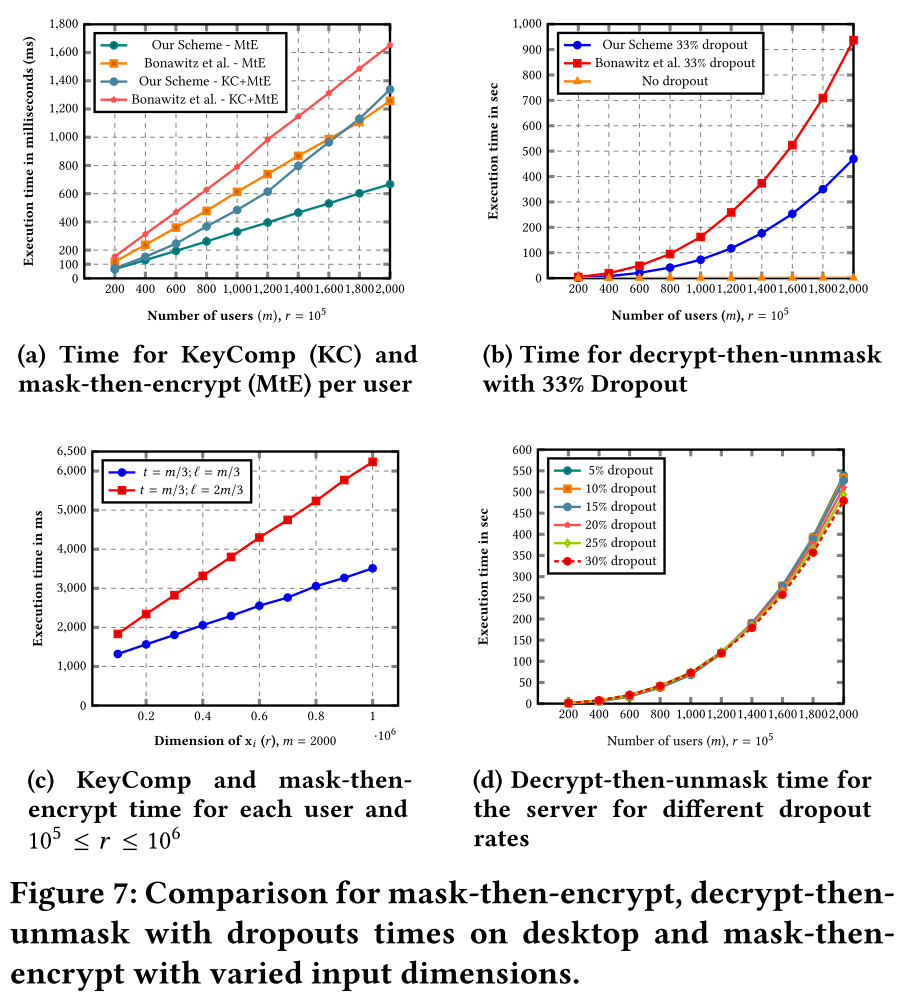
• 协议在电脑上的性能

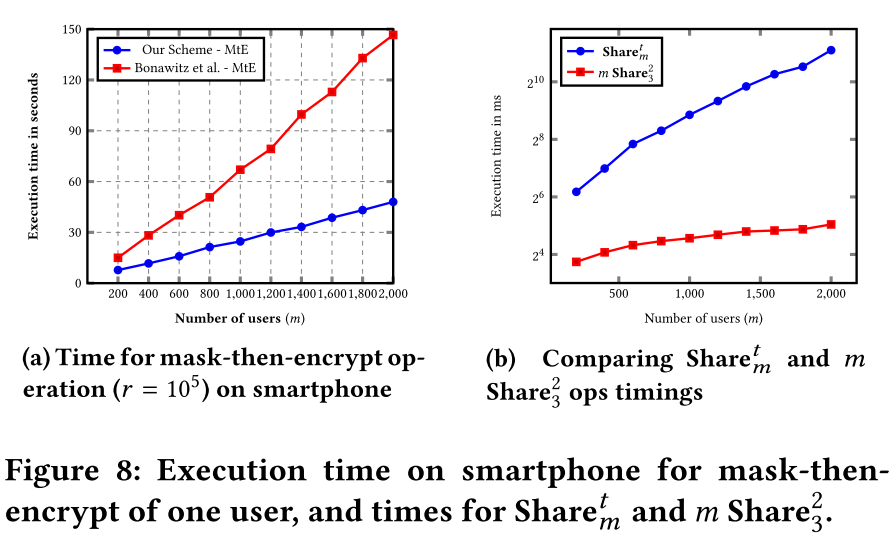
• 协议在手机上的性能

总结

本文提出了一个系统，该系统允许服务器以隐私保护的方式执行来自移动用户的高维输入的聚合总和，并且通信和计算开销较低。 我们通过将成对密钥生成任务外包给由两个 SSP 实现的密码服务提供商，使成对密钥生成任务成为非交互式的，从而节省了二次方的通信成本。 我们设计了一种聚合和协议，该协议具有较低的通信和计算开销，并能抵抗故障恢复场景。 对该方案的安全性和性能进行了分析。 我们通过对高维输入进行实验来评估和比较我们的方案在智能手机和台式电脑上的性能。 我们的实验表明，我们的方案比现有方案更快。

在 mask-then-encrypt 操作中，每个用户都需要执行一个 $Share_m^t$ 操作，而对于大规模网络，这对于移动设备来说计算量很大。我们将此作为一个悬而未决的问题，即如何消除 (t,m)-tss 操作，同时保证方案中的 (掉线场景) 健壮性和安全性。

参考

1. Secure Aggregation