论文英文名字	Understanding Distributed Poisoning Attack in Federated Learning
论文中文名字	了解联邦学习中的分布式投毒攻击
作者	Di Cao, Shan Chang, Zhijian Lin, Guohua Liu, Donghong Sun
来源	25th ICPADS 2019: Tianjin, China
年份	2019年12月
作者动机	（1）多个攻击者的分布式投毒是否比单个攻击者的传统投毒更有效（在总数相同的投毒训练样本下）？（2）攻击者和投毒样本的数量如何影响攻击成功率？（进一步提出防御机制）
阅读动机
创新点	利用欧几里得距离选择客户端构造无向图，并寻找最大团作为诚实用户集合

内容总结

本文的主要贡献

针对不同数量的攻击者和投毒的训练样本发起了翻转标签的投毒攻击，并检查了相应的攻击成功率。
提出了一种名为 Sniper 的方案，供服务器识别一组诚实的本地模型，以便可以使用它来聚合干净的全局模型。

定义

攻击成功率
如果投毒模型对于源标签 I 输出期望的目标标签 T，则攻击成功，否则攻击失败。对于模型 M，攻击的成功率 SR 给出为：
公式1

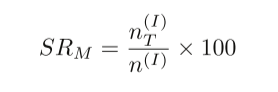
分布式投毒策略

实验设置

实验数据集：手写数字图像数据集 MNIST
实验攻击目标：（1）给定数字图像 6，模型输出 2；（2）：给定数字图像为 8，模型输出为 4。
实验模型：卷积神经网络（CNN）（请参阅下表中的体系结构），它具有四个卷积层和一个完整的连接层，并使用Relu作为前四层的激活函数，并使用Softmax作为输出的激活函数层
实验参数设置：将 betch_size 设置为 10。学习率 η 以 0.098 的指数速率从 0.08 衰减。此外添加了正则化项（λ = 0.01）以防止模型过度拟合。将模型中每个神经元的权重初始化为从正态分布 N(0, 0.022) 采样的随机值，并将偏差初始化为 0。

基准联邦学习系统

在基准系统中，所有参与者都是诚实的，仅使用干净的训练样本来一起训练全局模型。全局模型的准确性几乎为 100％。但是，如果参与者在不与他人共享参数的情况下训练本地模型，则本地模型的准确性约为 90％。这表明本地模型的聚合确实导致了更好的全局模型。

分布式投毒攻击的影响因素

实验结果
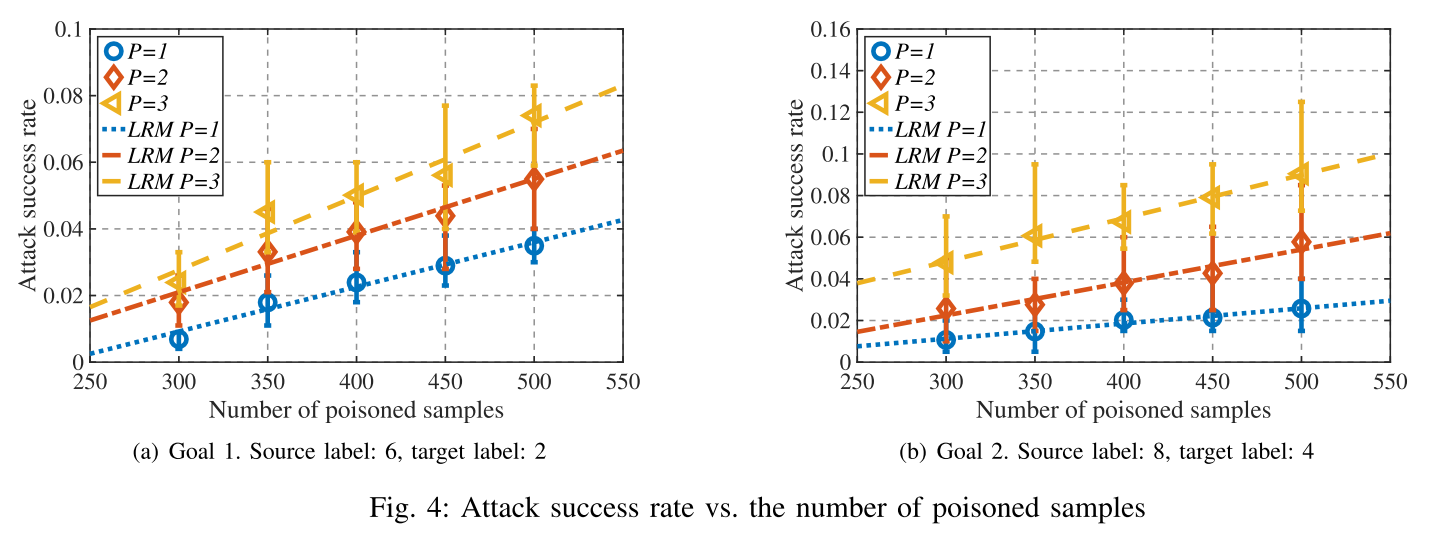
根据以上实验和分析提出以下命题：

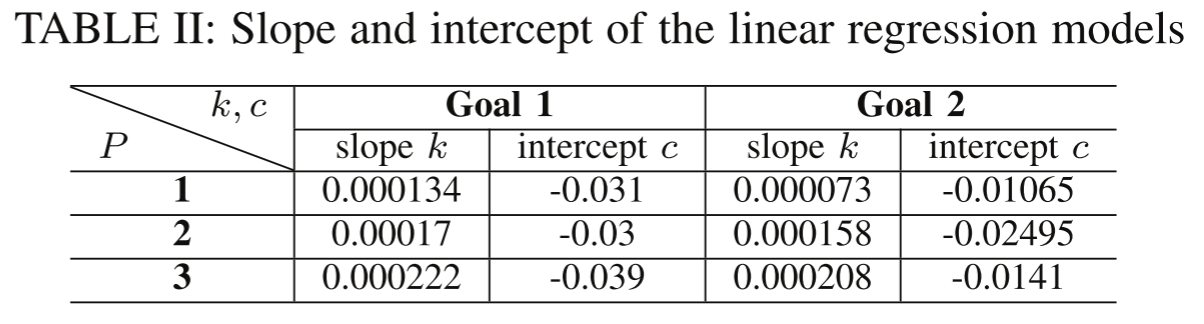
攻击成功率随投毒样本数量线性增加。
增加攻击者数量可以提高攻击成功率，而无需更改投毒样本的数量。
LRM 的斜率（即，提高攻击成功率的速度）随攻击者数量的增加而增加。

影响分析：

投毒样本数量的影响：投毒样本增加意味着投毒的全局模型与良性模型有很大的偏差。结果，聚合向量 agg 远离诚实向量，这意味着较高的攻击成功率。
攻击者数量的影响：全局模型聚合中涉及了更多的投毒本地模型。此外，将投毒样本分发给更多攻击者也意味着服务器更难识别每个投毒本地模型。投毒攻击的效率也提高了（攻击成功率提高）

Sniper 过滤机制

算法流程

第一，在从 N 个参与者收集本地模型 $ M_i $ 之后，服务器计算每对本地模型之间的欧几里得距离，即 $ Dis(M_i, M_j) $ 。
第二，服务器为 $ \gamma $ 赋一个初始值（根据实验结果，将 $ \gamma $ 设置为 0.5）。然后，它构造一个图，使得每个本地模型 $ M_i $ 都指向图中的顶点 $ v_i $ ，并且如果 $ M_i $ 与 $ M_j $ 之间的欧几里得距离小于预定阈值 $ \gamma $ ，则它们之间存在边 $ e_{i,j} $ 。
第三，服务器在图中找到最大团，并检查团中的顶点数是否大于 $ N/2 $ 。如果是这样，则服务器使用等式在团中聚合顶点（本地模型），并获得全局模型。否则，用增加 $ \gamma $ ，然后转到第二步。

算法图：

算法2

性能评估

算法效果

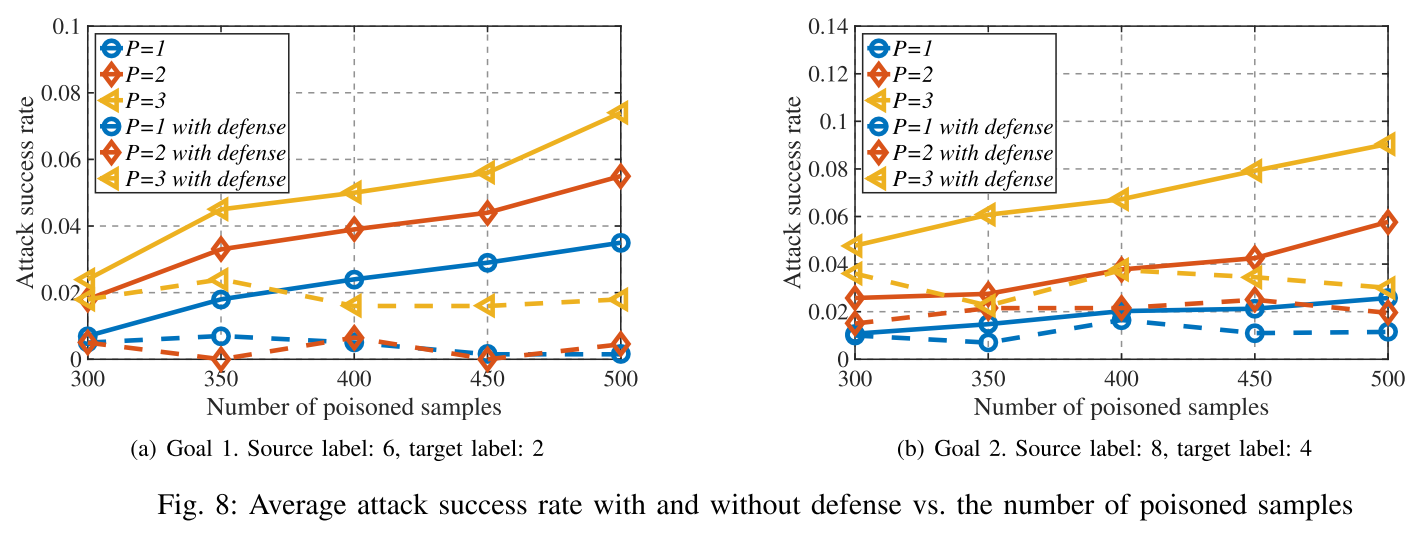
总结

在本文中分析了投毒样本数量和攻击者数量如何影响变量投毒攻击的性能。攻击成功率随投毒样本数量线性增加；在投毒样本数量不变的情况下，攻击成功率随攻击者数量的增加而增加，而涉及更多的攻击者时，增加的速度会更快。
通过观察模型之间的距离，发现诚实用户和攻击者的模型处于不同的团。基于此提出了一种过滤防御机制 Sniper。在每次通信期间，参数服务器都会运行它以过滤攻击者更新的参数。结果，即使在联邦学习系统中有多个攻击者，Sniper 仍可以识别诚实用户并显着降低攻击成功率。
将来会在联邦学习中评估更多的聚合算法，并分析多任务投毒攻击如何攻击全局模型。此外将通过增加客户数量来扩大联邦学习的规模。

参考

了解联邦学习中的分布式投毒攻击

会议记录

明确论文解决的问题
学习论文涉及的相关知识

Understanding Distributed Poisoning Attack in Federated Learning