论文英文名字	Secure Single-Server Aggregation with (Poly)Logarithmic Overhead
论文中文名字	具有（多）对数开销的安全单服务器聚合
作者	James Henry Bell, Kallista A. Bonawitz, Adrià Gascón, Tancrède Lepoint, Mariana Raykova
来源	27th CCS 2020: Virtual Event, USA
年份	2020年10月
作者动机	（1）secure aggregation 效率太低，如何在保证安全的情况下去提升效率？ （2）shuffle model 开销大，如何去降低开销？
阅读动机
创新点	图生成算法

内容总结

预备知识

• 简单图：不含平行边也不包含自环的图称为简单图。
• 完全图：完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。
• 正则图：各顶点的度均相同的无向简单图。
• k-连通图：对于连通图 G，其连通度 K(G) >= k。换言之，对于 k-连通图 G，不存在大小为 k-1 的点集 S，使得 G-S 不连通。（没有孤立点，任意两个顶点间有至少一条通路）

本文的主要贡献

• 在 semi-honest 场景下的 secure aggregation
• 在 malicious 场景下的 secure aggregation
• 将 secure shuffling 操作转换为 secure aggregation 操作

参数

the semi-honest protocol

半诚实的（诚实但好奇的，被动的）敌手：敌手诚实的遵守协议，但也会试图从接收到的信息中学习更多除输出以外的信息。
整体思路：先生成符合要求的无向图，再基于该无向图执行 summation 算法

• 无向图生成算法
  每个客户端要与其他 k 个客户端相连，相当于要构建一个有 n 个顶点的 k 连通无向图。在这个无向图里，每个顶点相当于一个客户端；每条边连接着的 2 个顶点意味着这 2 个客户端可以通过服务器交换协议中的私有信息（服务器无法获知信息内容）。（可以由服务器生成无向图）
  
  该无向图应该同时满足3个性质：
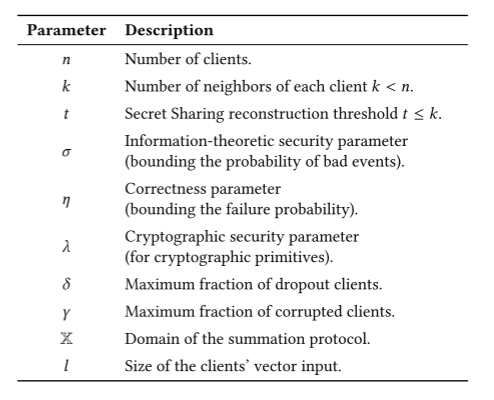
  （1）E1：不能有太多腐败的（即被黑客控制的）邻居节点
  第 i 个客户端中腐败的邻居节点的数量 $X_i \sim H(n-1, \gamma n, k)$，满足 E1 的概率为：$P(X_i < t)$。
  
  （2）E2：当一些客户端掉线以后，依然可以保证整个图的连通性，也就是没有被孤立的节点
  构建一个有 n 个顶点的 k 连通 Harary 图（在所有 n 顶点的 k 连通图里，Harary 图的边数量最小）
  根据 Harary 图的性质，要将一个顶点孤立，至少得去除它一半的边。在这个例子里，一个客户端被孤立，相当于它有 $k/2$ 个邻居节点都不受控制了（要么是掉线了，要么被黑客控制了），因此满足E2的概率为 $1-(\gamma + \delta)^{k/2}$。
  
  （3）E3：不能有太多掉线的邻居节点，否则没有足够多的邻居节点来进行秘密重建(1 ≤ t ≤ k)
  第 i 个客户端没有掉线的邻居节点数量 $Y_i \sim H(n-1, (1-\delta)n, k)$，满足 E3 的概率为：$P(Y_i > t)$。
  
       

• 聚合协议
  （1）利用上述的无向图生成算法生成一个有 n 个顶点的 k 连通无向图，并计算出对应的 t 和 k；
  
  （2）每个客户端 i 生成密钥对 1 和密钥对 2，将公钥 1 和公钥 2 通过服务器发往该客户端的k个邻居节点
  
  （3）每个客户端 i 生成随机种子 $b_i$ ，使用秘密分享计算出将 $b_i$ 和 sk1 分享给 k 个邻居节点对应的密文 $h^b$ 和 $h^s$ （总共是2k个不一样的密文），将 shares 加密后发给服务器
  
  （4）服务器判断此时没有准时到达的客户端数量（没有准时到达即可认为该客户端掉线了），如果超过了设置的阈值则终止。否则将各个客户端发来的密文和收件 id 发到指定的客户端（如果收件 id 对应的客户端掉线了，则不发送该消息）
  
  （5）把掉线的客户端去除，剩下的客户端里，每个客户端 i 与其每个邻居节点 j 使用 i 的私钥 1 和 j 的公钥 1 生成一个随机种子 $s_{ij}$，然后将输入与掩码相加后的结果 $y_i$ 发给服务器
  
  (6)服务器将每个客户端发来的 $y_i$ 收集起来，再次判断没有准时发来消息的客户端数量，如果超过了阈值就停止，否则将每个客户端 i 的目前仍没有掉线的邻居节点名单 R1 以及在第3步之后才掉线的邻居节点名单 R2 发给客户端 i（前一个名单 R1 是为了分享客户端i的随机种子，这样 i 的邻居节点可以在 i 掉线后计算出 b，后一个名单 R2 是为了恢复掉线客户端的 s）
  
  (7)目前在线的客户端i接受服务器发来的名单 R1 和 R2，客户端 i 用私钥 2 将第 3 步中从客户端 j 收到的密文解密，获得 j 对应的 $h^b$ 和 $h^s$，然后通过服务器向 R1 里的节点发送对应的 $h^b$ ，向R2里的节点发送对应的 $h^s$
  
  (8)服务器接受客户端发来的消息，再再次判断此时掉线的客户端数量是否超过阈值，是的话就终止；否则
  对于服务器收到 $y_i$ 消息的客户端 i，判断 i 邻居节点收到 i 发送的分享数量，如果该数量小于秘密分享要求的 t，则停止，否则就利用 i 邻居节点的分享恢复 i 的 $r_i$
  对于掉线的客户端 i ，判断 i 邻居节点收到 i 发送的分享数量，如果该数量小于秘密分享要求的 t，则停止，否则就利用i邻居节点的分享恢复 $s_{ij}$
  最后将 ${A_2}^\prime$ 名单里的客户端 i 对应的内容加起来，即可得到最终结果。
  
   
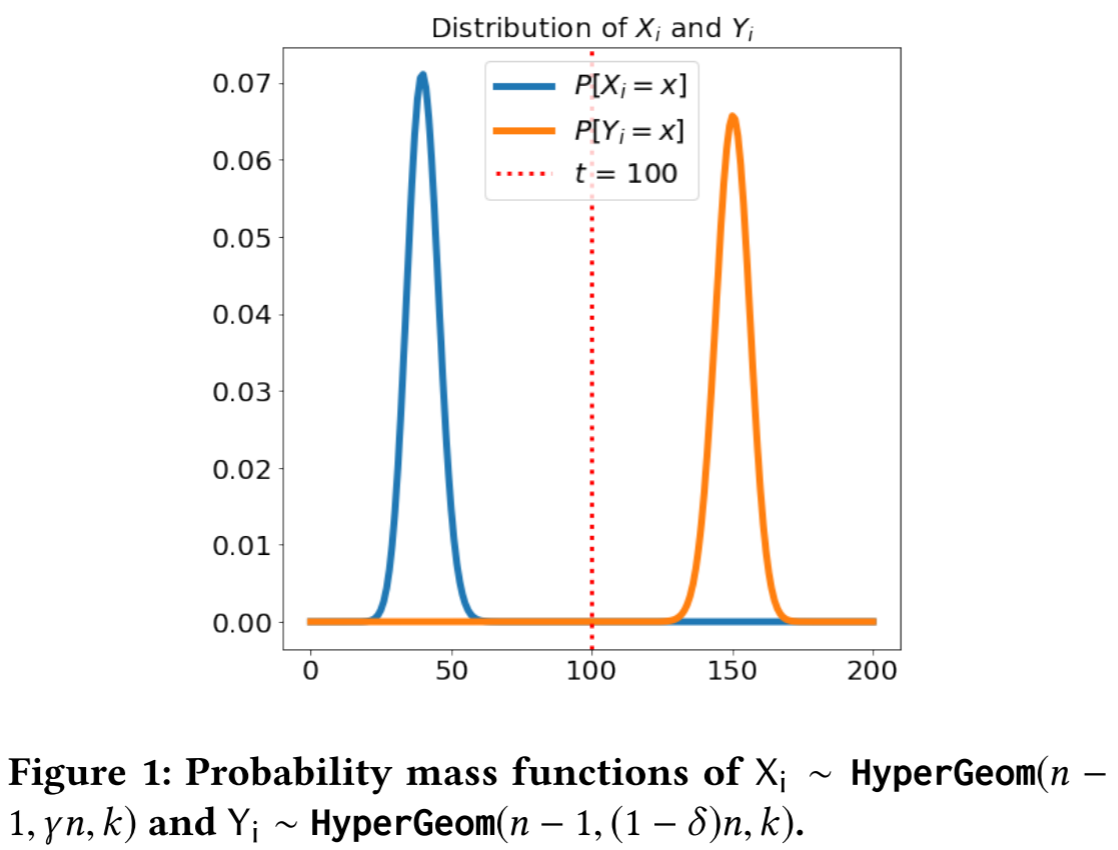
• 性能开销
  假设各种基本操作的时间复杂度都是$O(1)$，$k=O(\log n)$，$l$ 是指客户端的输入向量长度。
  客户端计算：$O(\log^2 n + l\log n)$
  客户端通信：$O(\log n + l)$
  服务器计算：$O(n\log^2 n + nl\log n)$
  服务器通信：$O(n\log n + nl)$
• 实验结果
  

the malicious protocol

恶意的（主动的）敌手：敌手不遵守协议，可以执行任意的攻击行为。
整体思路：先帮各个客户端交换密钥，再生成有向图，最后执行 summation 算法

• 交换密钥
  （1）每个客户端生成 2 对密钥，将 pk1 和 pk2 发送给服务器；
  （2）服务器将收到的公钥放到 Merkle tree 上面。（Merkle tree 是一种存着哈希值的数据结构，作用是用来验证自己收到的数据和发件人发的数据是否一致）

• 有向图生成算法
  （一个分布式图生成协议）
  （1）E4：在每个客户端单方面信任的客户端集合里，腐败的客户端数量不能太多。
  （2）E5：每个客户端的“交际圈”不能小于一定的比例 $\alpha$，不然容易被骗。
  （3）E6：确保有足够多的邻居节点来接收秘密分享的内容。
  
  具体方法
  (1) 每个客户端 i 随机选择 k 个客户端作为信任的对象，并将 outgoing 发给服务器
  (2) 服务器收到后将 (信任 i 的客户端 id, pk1, pk2 ) 发给客户端 i，并发送每个客户端 i 的邻居节点（包括信任 i 的客户端以及 i 信任的客户端）和 $ \log_2^n $ 的哈希值，用于 Merkle tree 验证
  (3) 客户端 i 要是收到了超过 4k 个密钥（说明里面包含了伪造的客户端密钥），则终止。否则用 Merkle tree 验证收到的公钥的正确性和是否收到 outgoing 中每个客户端的公钥

• 聚合协议
  （1）每个客户端 i 生成随机种子 $b_i$ ，使用秘密分享计算出将 $b_i$ 和 sk1 分享给 k 个邻居节点对应的密文 $h^b$ 和 $h^s$ （总共是 2k 个不一样的密文），将 shares 加密后发送给服务器
  
  （2）服务器判断此时没有准时到达的客户端数量（没有准时到达即可认为该客户端掉线了），如果超过了设置的阈值则终止。否则将各个客户端发来的密文和收件 id 发到指定的客户端（如果收件 id 对应的客户端掉线了，则不发送该消息）
  
  （3）把掉线的客户端去除，对于剩下的客户端 i
  每个客户端 i 与其每个邻居节点 j 使用 i 的 sk1 和 j 的 pk1 生成一个随机种子 $s_{ij}$，然后计算输入与掩码相加后的结果 $y_i$
  使用 sk2 将（字符串“included”，客户端 i 的 id，客户端 j 的 id）进行签名
  将（y，m，签名）发送给服务器
  
  （4）服务器将每个客户端发来的信息收集起来，再次判断没有准时发来消息的客户端数量，如果超过了阈值就停止，否则将每个客户端 i 的目前仍没有掉线的且信任 i 的客户端名单 R1，在第 6 步之后才掉线的且信任 i 的客户端名单 R2，以及对应的 (m, $\sigma$) 发给客户端 i
  
  （5）每个没掉线的客户端确认 R1 和 R2 相交是否为空集，确认 R1 和 R2 里的客户端是不是都信任 i（这是为了确保服务器没有把虚构的客户端加进来），再利用 Merkel tree 确认签名是否都有效
  
  （6）客户端 i 对每个信任 i 的客户端 j,用 i 的 sk2 加密 (“ack”, i, j) 形成密文 m，再将 (m, $\sigma$) 通过服务器发送给客户端 j
  
  （7）服务器确认目前掉线的客户端数量是否超过阈值，超过则终止，否则将 (m, $\sigma$) 发送给对应的客户端
  
  （8）客户端收到信息后验证信息是否有效，有效则
  客户端 j 通过服务器向 j 信任的每个客户端发送 (i, $h^b$)，其中 i 为 R1 名单里的每个客户端
  客户端 j 通过服务器向 j 信任的每个客户端发送 (i, $h^s$)，其中 i 为 R2 名单里的每个客户端
  
  （9）服务器确认目前掉线的客户端数量是否超过阈值，超过则终止，否则
  • 对于 R1 名单里的客户端 i，判断 i 邻居节点收到 i 发送的 $h^b$ 数量，如果该数量小于秘密分享要求的 t，则停止，否则就利用 i 邻居节点的 $h^b$ 恢复 i 的随机种子 $b_i$（这里是为了在第 3 步中把加了双掩码的输入发给了服务器的客户端，输入中对应的 $F(b_i)$ 给抵消掉）
  • 对于 R2 名单里的客户端 i，判断 i 邻居节点收到 i 发送的 $h^s$ 数量，如果该数量小于秘密分享要求的 t，则停止，否则就利用 i 邻居节点的 $h^s$ 恢复 i 的 sk1，从而恢复 \( s_{ij} \) (这里是将掉线的 $F(s_{ij})$ 抵消掉)
  • 最后将 R1 名单里的客户端 i 对应的内容加起来，即可得到最终结果
    
     
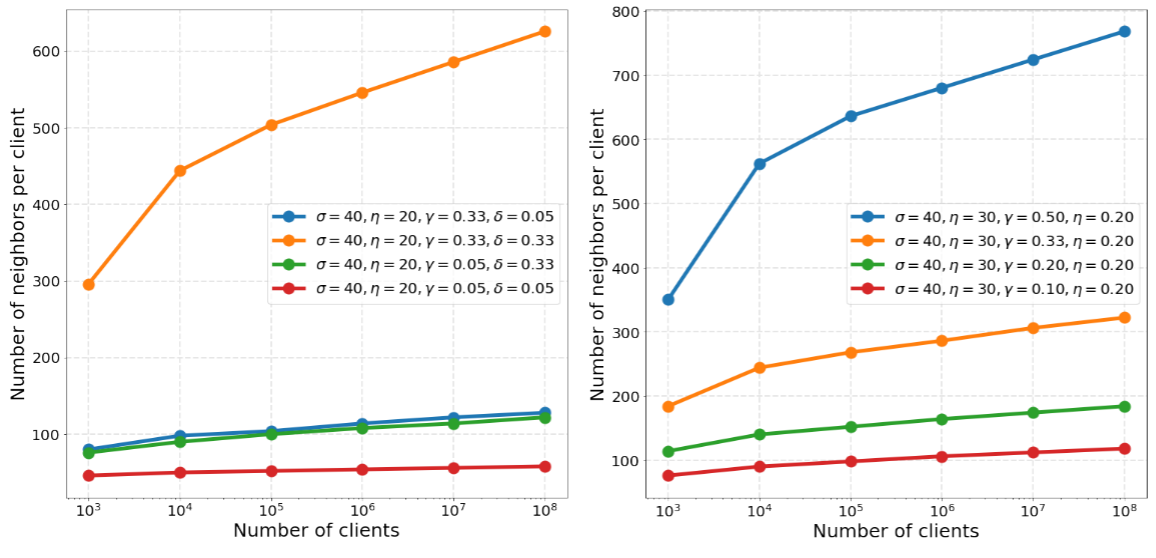
• 性能开销
  假设各种基本操作的时间复杂度都是$O(1)$，$k=O(\log n)$，$l$ 是指客户端的输入向量长度。
  客户端计算：$O(\log^2 n + l\log n)$
  客户端通信：$O(\log n + l)$
  服务器计算：$O(n\log^2 n + nl\log n)$
  服务器通信：$O(n\log n + nl)$
• 实验结果
  

secure shuffling

因为实现 shuffling 需要利用可信的计算硬件或者类似于洋葱路由那样的混合网络，而利用上述的 summation 算法来实现 secure shuffling 操作，这样可以避免引入新的计算开销和通信开销。
这里引入了一种数据结构 IBLT：invertible Bloom lookup table ，IBLT里的每个元素存着（key，value）。2 个 IBLT 相加相当于对 2 个 IBLT 的元素求并集。

• 具体实现方法
  (1) 每个客户端都创建一个新的 IBLT，并从一个集合里选取一个随机数作为 key（为了避免跟其他客户端选到了同一个随机数，这个集合得大一点，比如 $2^{64}$ 这种量级），然后将要发送的内容作为 value，将（key，value）插入到 IBLT 中
  (2) 服务器对每个客户端发来的 IBLT 进行 summation（最终会得到一个 IBLT，在这个 IBLT 里无法根据 key 或者 value 来推出发送方是谁，从而实现了 shuffling 操作）

参考

1. Secure Single-Server Aggregation with (Poly)Logarithmic Overhead